Outline numerics used in the code

Differentiation

FIXME is a node-based, collocated finite difference code and the derivatives are to be evaluate on the nodes, based on nodal values. Let 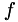$f$ be a vector of field values to be differentiated and let 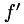$f'$ be its derivative. The differentiation occurs along coordinate lines using the generic stencil

$\beta f'_{i-2} + \alpha f'_{i-1} + f'_i + \alpha f'_{i+1} + \beta f'_{i+2} = \sum_{j=-N}^N a_j f_{i+j}$

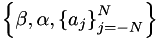where $\left\{\beta, \alpha, \left\{a_j\right\}_{j=-N}^N\right\}$ are the coefficients of the particular scheme being used. For SPACEDISC = EXPLICIT we take 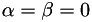$\alpha = \beta = 0$ . The coefficients are specified in ModInput.f90. For boundary schemes, biased stencils are used whose coefficients are also specified in ModInput.f90. Many schemes can be found in Lele[1].

Todo:: Find specific functions for coefficients

Computation of the metrics

Following Visbal & Gaitonde[3] we compute the metrics in a manner to (mostly) preserves the geometric conservation law. The manner in which the metrics are computed depends on the problem dimension. For 2D we have

$\begin{aligned} \hat{\xi}_x &= \frac{\partial y}{\partial \eta}, \quad \hat{\xi}_y = -\frac{\partial x}{\partial \eta} \\ \hat{\eta}_x &= -\frac{\partial y}{\partial \xi}, \quad \hat{\eta}_y = \frac{\partial x}{\partial \xi} \end{aligned}$

while for 3D we have

$\begin{aligned} \hat{\xi}_x &= \frac{\partial}{\partial \zeta}\left(\frac{\partial y}{\partial \eta}z\right) - \frac{\partial}{\partial \eta}\left(\frac{\partial y}{\partial \zeta}z\right) \\ \hat{\xi}_y &= \frac{\partial}{\partial \zeta}\left(\frac{\partial z}{\partial \eta}x\right) - \frac{\partial}{\partial \eta}\left(\frac{\partial z}{\partial \zeta}x\right) \\ \hat{\xi}_z &= \frac{\partial}{\partial \zeta}\left(\frac{\partial x}{\partial \eta}y\right) - \frac{\partial}{\partial \eta}\left(\frac{\partial x}{\partial \zeta}y\right) \end{aligned}$

for the first coodinate,

$\begin{aligned} \hat{\eta}_x &= \frac{\partial}{\partial \xi}\left(\frac{\partial y}{\partial \zeta}z\right) - \frac{\partial}{\partial \eta}\left(\frac{\partial y}{\partial \xi}z\right) \\ \hat{\eta}_y &= \frac{\partial}{\partial \xi}\left(\frac{\partial z}{\partial \zeta}x\right) - \frac{\partial}{\partial \eta}\left(\frac{\partial z}{\partial \xi}x\right) \\ \hat{\eta}_z &= \frac{\partial}{\partial \xi}\left(\frac{\partial x}{\partial \zeta}y\right) - \frac{\partial}{\partial \eta}\left(\frac{\partial x}{\partial \xi}y\right) \end{aligned}$

for the second coodinate, and

$\begin{aligned} \hat{\zeta}_x &= \frac{\partial}{\partial \eta}\left(\frac{\partial y}{\partial \xi}z\right) - \frac{\partial}{\partial \xi}\left(\frac{\partial y}{\partial \eta}z\right) \\ \hat{\zeta}_y &= \frac{\partial}{\partial \eta}\left(\frac{\partial z}{\partial \xi}x\right) - \frac{\partial}{\partial \xi}\left(\frac{\partial z}{\partial \eta}x\right) \\ \hat{\zeta}_z &= \frac{\partial}{\partial \eta}\left(\frac{\partial x}{\partial \xi}y\right) - \frac{\partial}{\partial \xi}\left(\frac{\partial x}{\partial \eta}y\right) \end{aligned}$

for the third coodinate.

In both cases the inverse Jacobian is

$J^{-1} = \left|\frac{\partial x_i}{\partial \xi_j}\right|$

with $J = 1/J^{-1}$ .