In fluid domains, the code solves the compressible Navier-Stokes equations in curvilinear coordinates. The basic equations, in a cartesian coordinate space, for the conserved mass density 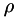 , momentum density
, momentum density 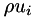 , and total energy density
, and total energy density 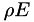 are, in index form with summation convention are given as
are, in index form with summation convention are given as
![\[ \begin{align} \frac{\partial \rho}{\partial t} + \frac{\partial }{\partial x_j} \rho u_j &= S_\rho \\ \frac{\partial \rho u_i}{\partial t} + \frac{\partial}{\partial x_j}\left(\rho u_i u_j + p\delta_{ij} - \tau_{ij}\right) &= S_{\rho u_i} \\ \frac{\partial \rho E}{\partial t} + \frac{\partial}{\partial x_j}\left(\left\{\rho E + p\right\}u_j + q_j - u_i \tau_{ij}\right) &= S_{\rho E} \end{align} \]](form_17.png)
where 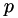 is the thermodynamic pressure,
is the thermodynamic pressure, 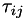 is the viscous stress tensor, and
is the viscous stress tensor, and 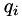 is the heat flux in the
is the heat flux in the 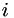 th direction.
th direction. 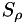 ,
, 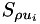 , and
, and 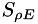 are are mass, momentum, and energy density source terms. These equations can be written in the compact form
are are mass, momentum, and energy density source terms. These equations can be written in the compact form
![\[ \frac{\partial Q}{\partial t} + \frac{\partial \vec{F}_j}{\partial x_j} = S \]](form_25.png)
where ![$Q = [\rho\,\rho \vec{u}\,\rho E]^T$](form_26.png) is the vector of conserved variables,
is the vector of conserved variables, 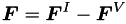 is the flux vector account for both visicd and invisci terms, and
is the flux vector account for both visicd and invisci terms, and 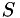 is the source term vector. The so-called RHS
is the source term vector. The so-called RHS 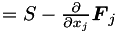 is evaluated by the top-level RHS driver function in include/EulerRHS.H.
is evaluated by the top-level RHS driver function in include/EulerRHS.H.
The viscous stress tensor is defined as
![\[ \tau_{ij} = \mu \left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) + \lambda \frac{\partial u_k}{\partial x_k}\delta_{ij} \]](form_30.png)
where 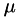 and
and 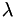 are the first and second coefficients of viscosity, respectively; both may be a function of temperature. Note that Stokes' hypothesis
are the first and second coefficients of viscosity, respectively; both may be a function of temperature. Note that Stokes' hypothesis 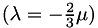 is not automatically enforced and that
is not automatically enforced and that 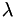 is related to bulk viscosity
is related to bulk viscosity 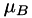 as
as 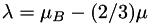 .
.
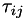 is computed by ComputeTauBuffer in src/ViscidUtil.C.
is computed by ComputeTauBuffer in src/ViscidUtil.C.
The heat flux vector is defined as
![\[ q_i = - \kappa \frac{\partial T}{\partial x_i} \]](form_36.png)
where 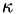 is the thermal conductivity. The heat flux vector,
is the thermal conductivity. The heat flux vector, 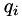 , is computed by ComputeHeatFluxBuffer in src/ViscidUtil.C.
, is computed by ComputeHeatFluxBuffer in src/ViscidUtil.C.
The first viscosity coefficient 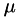 , bulk viscosity coefficient,
, bulk viscosity coefficient, 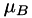 , and the thermal conductivity
, and the thermal conductivity 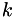 depend on the thermodynamic state of the fluid. Currently, only one implementation is available, although others can be easily implemented in ViscidUtil.C.
depend on the thermodynamic state of the fluid. Currently, only one implementation is available, although others can be easily implemented in ViscidUtil.C.
The Power Law transport model in implemented in ComputeTVBufferPower.
The power law model gives the dynamic viscosity, 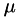 as
as
![\[ \mu = \beta T^n \]](form_39.png)
where 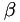 and
and 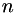 are user specified parameters, typically
are user specified parameters, typically 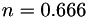 and
and 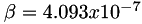 for air.
for air.
The bulk viscosity is defined as
![\[ \mu_B = \alpha \mu \]](form_44.png)
where 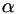 is a user specified parameter, typically
is a user specified parameter, typically 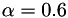 for air.
for air.
Thus the second coefficient of viscosity can be calculated as
![\[ \lambda = \left(\alpha - 2/3\right) \mu \]](form_47.png)
The power law model calculates the :w
The equations of state provides closure by relating the intensive state variables, pressure and temperature, to the extensive state variables, specific internal energy and volume. Currently, only one implementation is available, although others can be easily implemented in EulerUtil.C.
The equation of state currently available is that of an ideal gas, assuming constant specific heats. The equations of state are
![\[ P = \rho R T \]](form_48.png)
where 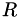 is the specific gas constant, defined as
is the specific gas constant, defined as 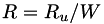 with
with 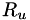 the universal gas constant, and
the universal gas constant, and 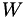 the molecular weight.
the molecular weight.
The specific heat capacity at constant volume and pressure are defined as
![\[ \begin{align} C_v &= \left(\frac{\partial E}{\partial T}\right)_v \\ C_p &= \left(\frac{\partial H}{\partial T}\right)_p \end{align} \]](form_53.png)
Then, by substitution into the equation of state we get the following relation
![\[ R = C_p - C_v \]](form_54.png)
By defining the specific heat ratio, 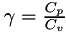 , the following expressions give the realtionship between specific energy, pressure, and temperature as implemented by ComputeDVBufferIdeal.
, the following expressions give the realtionship between specific energy, pressure, and temperature as implemented by ComputeDVBufferIdeal.
![\[ \begin{align} P &= (\gamma -1) \rho e \\ T &= \frac{\gamma-1}{R} e \end{align} \]](form_56.png)
PlasCom2 can run in either a dimensional or non-dimensional mode. The code uses the following variables to define the non-dimensional scaling:
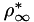 ,
, 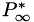 ,
, 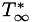 , and
, and 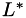 , a length scale. Where
, a length scale. Where  denotes a dimensional value and
denotes a dimensional value and 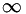 denotes the reference state. There are two optional non-dimensional spaces available to the user, as shown in the table below.
denotes the reference state. There are two optional non-dimensional spaces available to the user, as shown in the table below.
| Standard (nonDimensional=1) | Legacy PlasComCM (nonDimensional=2) |
|---|---|
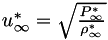 | 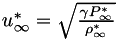 |
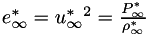 | 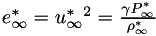 |
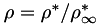 | 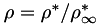 |
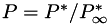 | 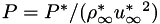 |
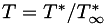 | 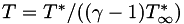 |
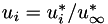 | 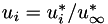 |
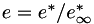 | 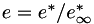 |
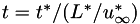 | 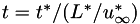 |
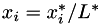 |
|
Substitution into the dimensional form of the Navier-Stokes equations yields the non-dimensional equivalent
![\[ \begin{align} \frac{\partial \rho}{\partial t} + \frac{\partial }{\partial x_j} \rho u_j &= S_\rho \\ \frac{\partial \rho u_i}{\partial t} + \frac{\partial}{\partial x_j}\left(\rho u_i u_j + p\delta_{ij} - \tau_{ij}\right) &= S_{\rho u_i} \\ \frac{\partial \rho E}{\partial t} + \frac{\partial}{\partial x_j}\left(\left\{\rho E + p\right\}u_j + q_j - u_i \tau_{ij}\right) &= S_{\rho E} \end{align} \]](form_17.png)
with the following non-dimensionalization for the source terms
![\[\begin{align} S_\rho &= \frac{S^*_\rho L^*}{\rho^*_\infty U^*_\infty} \\ S_{\rho u_i} &= \frac{S^*_{\rho u_i } L^*}{\rho^*_\infty U^*_\infty^2 } \\ S_{\rho E} &= \frac{S^*_{\rho E} L^*}{\rho^*_\infty U^*_\infty^3} \end{align} \]](form_76.png)
by choosing the following non-dimensionalizations for the transport coefficients
![\[\begin{align} \mu &= \mu^* /\mu^*_\infty \\ \lambda &= \lambda^* /\lambda^*_\infty \\ \kappa &= \kappa^* /\kappa^*_\infty \\ \end{align} \]](form_77.png)
the non-dimensional viscous stress tensor and heat flux vector can be written as
![\[\begin{align} \tau_{ij} &= \frac{\mu}{\RE} \left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) + \frac{\lambda}{\RE} \frac{\partial u_k}{\partial x_k}\delta_{ij} \\ q_i &= - \frac{\mu}{\RE \Pr} \frac{\partial T}{\partial x_i} \end{align} \]](form_78.png)
where 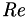 is defined as the code Reynolds number,
is defined as the code Reynolds number, 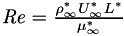 and
and 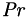 is defined as the Prandtl number,
is defined as the Prandtl number, 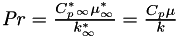 which define the dimensional reference values
which define the dimensional reference values 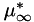 and
and 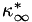 respectively.
respectively.
There are no special modifications to the calorically perfect gas equation of state, with the exception of the specific gas constant. The reference gas constant is calculated and non-dimensionalized as follows
![\[\begin{align} R^*_\infty &= \frac{P^*_\infty}{\rho^*_\infty T^*_\infty} \\ R &= R^* /R^*_\infty \\ \end{align} \]](form_84.png)
For the standard non-dimensionalization, 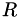 is exactly 1.0. For the legacy non-dimensionalization,
is exactly 1.0. For the legacy non-dimensionalization, 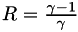 .
.
It is possible to express the Navier-Stokes equations in any other coordinate system 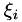 provided the mapping
provided the mapping 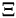 from
from 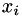 to
to 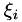 is given. The Cartesian coordinates
is given. The Cartesian coordinates 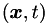 can be mapped to another coordinate system
can be mapped to another coordinate system 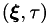 via the time-dependent mappings
via the time-dependent mappings
![\[ \vec{x} = {X}(\vec{\xi},\tau) \qquad \mbox{ with inverse } \qquad \vec{\xi} = \Xi(\vec{x},t) \]](form_91.png)
where 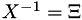 and we only consider non-singular mappings such that
and we only consider non-singular mappings such that 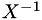 exists and is well defined. Moreover we take
exists and is well defined. Moreover we take 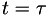 . The Jacobian of the transformation is defined as
. The Jacobian of the transformation is defined as 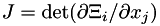 and is strictly positive.
and is strictly positive.
Under these conditions and with simple application of the chain rule it can be shown[2] that the vector (compact) form tranforms to
![\[ \frac{\partial}{\partial \tau}\left(\frac{Q}{J}\right) + \frac{\partial \hat{\vec{F}}^I_i}{\partial \xi_i} - \frac{\partial \hat{\vec{F}}^V_i}{\partial \xi_i}= \frac{S}{J} \]](form_96.png)
after using the identities
![\[ \begin{split} \frac{\partial}{\partial \xi_j}\left(\frac{1}{J}\frac{\partial \xi_j}{\partial x_i}\right) &= 0 \qquad \mbox{ for $i = 1, \dots, N$} \\ \frac{\partial}{\partial \tau}\left(\frac{1}{J}\right) + \frac{\partial}{\partial \xi_j}\left(\frac{1}{J}\frac{\partial \xi_j}{\partial t}\right) &= 0, \end{split} \]](form_97.png)
where 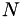 is the number of dimensions. If we define the weighted metric
is the number of dimensions. If we define the weighted metric 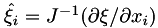 and contravariant velocity
and contravariant velocity 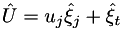 , with similar expressions for the remaining components, then the inviscid fluxes
, with similar expressions for the remaining components, then the inviscid fluxes 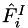 are
are
![\[ \hat{\vec{F}}^I_1 = \begin{bmatrix} \rho \hat{U} \\ \rho u \hat{U} + p\hat{\xi}_x \\ \rho v \hat{U} + p \hat{\xi}_y \\ (\rho E + p)\hat{U} - \hat{\xi}_t p \end{bmatrix}\qquad \mbox{ and } \qquad \hat{\vec{F}}^I_2 = \begin{bmatrix} \rho \hat{V} \\ \rho u \hat{V} + p\hat{\eta}_x \\ \rho v \hat{V} + p \hat{\eta}_y \\ (\rho E + p)\hat{V} - \hat{\eta}_t p \end{bmatrix} \]](form_102.png)
in two dimensions and
![\[ \hat{\vec{F}}^I_1 = \begin{bmatrix} \rho \hat{U} \\ \rho u \hat{U} + p\hat{\xi}_x \\ \rho v \hat{U} + p \hat{\xi}_y \\ \rho w \hat{U} + p\hat{\xi}_z \\ (\rho E + p)\hat{U} - \hat{\xi}_t p \end{bmatrix}, \quad \hat{\vec{F}}^I_2 = \begin{bmatrix} \rho \hat{V} \\ \rho u \hat{V} + p\hat{\eta}_x \\ \rho v \hat{V} + p \hat{\eta}_y \\ \rho w \hat{V} + p \hat{\eta}_z \\ (\rho E + p)\hat{V} - \hat{\eta}_t p \end{bmatrix}, \quad \mbox{and} \quad \hat{\vec{F}}^I_3 = \begin{bmatrix} \rho \hat{W} \\ \rho u \hat{W} + p\hat{\zeta}_x \\ \rho w \hat{W} + p \hat{\zeta}_y \\ \rho w \hat{W} + p \hat{\zeta}_z \\ (\rho E + p)\hat{W} - \hat{\zeta}_t p \end{bmatrix} \]](form_103.png)
The inviscid fluxes are computed dimension-at-a-time by Euler::Flux1D in kernels/Euler.f90.
The viscous fluxes may be expressed in a number of forms, depending on the particular goal. The main difference between the particular forms is how second derivatives are taken; namely, either 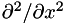 is taken directly or as two repeated derivatives,
is taken directly or as two repeated derivatives, 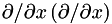 . The use of
. The use of 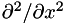 is advantageous in that it allows for the most physical dissipation in the code, as determined by the modified wavenumber. (See, e.g., Lele[1] for a discussion of the modified wavenumber and its meaning.) However, it is also expensive, especially in three or more dimensions. Using repeated derivatives in advantageous for two reasons: (i) it keeps the equations in conservative form which is useful for shock capturing and (ii) it is less expensive (by a factor around 2.5 in three dimensions) than the fully expanded form. However, it provides less physical dissipation, especially at the highest wavenumbers, exactly where it is most needed.
is advantageous in that it allows for the most physical dissipation in the code, as determined by the modified wavenumber. (See, e.g., Lele[1] for a discussion of the modified wavenumber and its meaning.) However, it is also expensive, especially in three or more dimensions. Using repeated derivatives in advantageous for two reasons: (i) it keeps the equations in conservative form which is useful for shock capturing and (ii) it is less expensive (by a factor around 2.5 in three dimensions) than the fully expanded form. However, it provides less physical dissipation, especially at the highest wavenumbers, exactly where it is most needed.
Following Anderson, Tanehill, and Pletcher (1984), the strong form of the viscous terms is as follows
![\[ \begin{align} \frac{\partial}{\partial t}\left(\frac{\rho u_1}{J}\right) &= \cdots \frac{\partial}{\partial \xi}\left(\hat{\xi}_i\tau_{i1}\right) + \frac{\partial}{\partial \eta}\left(\hat{\eta}_i\tau_{i1}\right) + \frac{\partial}{\partial \zeta}\left(\hat{\zeta}_i\tau_{i1}\right) \\ \frac{\partial}{\partial t}\left(\frac{\rho u_2}{J}\right) &= \cdots \frac{\partial}{\partial \xi}\left(\hat{\xi}_i\tau_{i2}\right) + \frac{\partial}{\partial \eta}\left(\hat{\eta}_i\tau_{i2}\right) + \frac{\partial}{\partial \zeta}\left(\hat{\zeta}_i\tau_{i2}\right) \\ \frac{\partial}{\partial t}\left(\frac{\rho u_3}{J}\right) &= \cdots \frac{\partial}{\partial \xi}\left(\hat{\xi}_i\tau_{i3}\right) + \frac{\partial}{\partial \eta}\left(\hat{\eta}_i\tau_{i3}\right) + \frac{\partial}{\partial \zeta}\left(\hat{\zeta}_i\tau_{i3}\right) \\ \frac{\partial}{\partial t}\left(\frac{\rho E}{J}\right) &= \cdots \frac{\partial}{\partial \xi}\left(\hat{\xi}_i [ u_j \tau_{ij} - q_i ]\right) + \frac{\partial}{\partial \eta}\left(\hat{\eta}_i [ u_j \tau_{ij} - q_i ]\right) + \frac{\partial}{\partial \zeta}\left(\hat{\zeta}_i [ u_j \tau_{ij} - q_i ]\right) \end{align} \]](form_106.png)
This form is much faster than the other forms, but does not have any dissipation at the highest wavenumbers. The viscous flux components are computed dimension-at-a-time by Viscid::StrongFlux1D in kernels/Viscid.f90.
Selected by the user with METRICTYPE = NONORTHOGONAL_STRONGFORM in .